Entropic system in the relativistic Klein-Gordon Particle

Authors

  • C. A. Onate Physics Programme, Department of Physical Sciences, Landmark University, Omu-Aran, Nigeria
  • M. C. Onyeaju Department of Physics, Theoretical Physics Group, University of Port Harcourt, Choba, Nigeria

Keywords:

Eigensolutions, Bound states, Wave equation, Theoretic quantity

Abstract

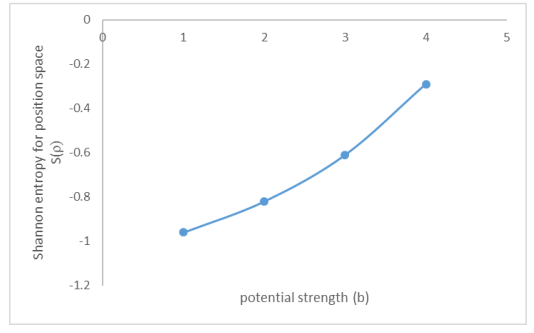
The solutions of Kratzer potential plus Hellmann potential was obtained under the Klein-Gordon equation via the parametric Nikiforov-Uvarov method. The relativistic energy and its corresponding normalized wave functions were fully calculated. The theoretic quantities in terms of the entropic system under the relativistic Klein-Gordon equation (a spinless particle) for a Kratzer-Hellmann’s potential model were studied. The effects of a and b respectively (the parameters in the potential that determine the strength of the potential) on each of the entropy were fully examined. The maximum point of stability of a system under the three entropies was determined at the point of intersection between two formulated expressions plotted against a as one of the parameters in the potential. Finally, the popular Shannon entropy uncertainty relation known as Bialynick-Birula, Mycielski inequality was deduced by generating numerical results.

Dimensions

C. E. Shannon, “A Mathematical Theory of Communication”, Bell System Technical Journal 27 (1948) 379-423.

J. S. Dehesa, A. Martinez-Finkelshtein & V. N. Sorokin, “Quantum-information entropies for highly excited states of single-particle systems with power-type potential”, Physical Review A 66 (2002) 062109.

J. O. A. Idiodi & C. A. Onate, “Entropy, Fisher Information and Variance with Frost-Musulin Potential”, Communications in Theoretical Physics 66 (2016) 269.

J. S. Dehesa, W. V. Assche & R. S. Yáñez, “Information entropy of classical orthogonal Polynomials and their application to the harmonic oscillator and Coulomb potential”, Methods and Applied Analysis 4 (1997) 91.

S. A. Najafizade, H. Hassanabadi & S. Zarrinkamar, “Nonrelativistic Shannon information entropy for Kratzer potential”, Chinese Physics B 25 (2016) 040301.

J. S. Dehesa, A. Martinez-Finkelshtein & V. N. Sorokin, “Information-theoretic measures for Morse and Pöschl–Teller potentials”, Molecular Physics 104 (2005) 613.

C. A. Onate, M. C. Onyeaju, A. N. Ikot, J. O. A. Idiodi & O. J. Ojonubah, “Eigen solutions, Shannon entropy and Fisher information under the Eckart Manning-Rosen potential model”, Journal of the Korean Physical Socciety 70 (2017) 339.

J. S. Dehesa, A. Martinez-Finkelshtein & J. Sánchez-Ruiz, “Quantum information entropies and orthogonal polynomials”, Journal of Computation and Applied Mathematics 133 (2001) 23.

C.A. Onate & J. O. A. Idiodi, “Fisher Information and Complexity Measure of Generalized Morse Potential Model”, Communications in Theoretical Physics 66 (2016) 275.

X. D. Song, G. H. Sun & S. H. Dong, “Shannon information entropy for an infinite circular well”, Physics Letters A 379 (2015) 1402.

S. A. Najafizade, H. Hassanabadi & S. Zarrinkamar, “Nonrelativistic Shannon information entropy for Killingbeck potential”, Canadian Journal of Physics 94 (2016) 1085.

S. A. Najafizade, H. Hassanabadi & S. Zarrinkamar, “Theoretical information measurement in nonrelativistic time-dependent approach”, Indian Journal Physics 92 (2018) 183.

C. A. Onate, A. N. Ikot, M. C. Onyeaju, O. Ebomwonyi & J. O. A. Idiodi, “Effect of dissociation energy on Shannon and Rényi entropies”, Karbala International Journal of Modern Science 4 (2018) 134.

W. A. Yahya, K. J. Oyewumi & S. D. Sen, “Position and momentum information-theoretic measures of the pseudoharmonic potential”, International Journal of Quantum Chemisrty 115 (2015) 1543.

C. A. Onate, O. Adebimpe, B. O. Adebesin & A. F. Lukman, “Information-theoretic measure of the hyperbolical exponential-type potential”, Turkish Journal of Physics 42 (2018) 402.

W. A. Yahya, K. J. Oyewumi & K. D. Sen, “Information and complexity measures for the ring-shaped modified Kratzer potential”, Indian Journal of Chemistry 53 (2014) 1307.

W. A. Yahya, K. J. Oyewumi & K. D. Sen, “Quantum information entropies for the `l-state Pöschl–Teller-type potential”, Journal of Mathematical Chemistry 54 (2018) 1810.

C. A. Onate, M. C. Onyeaju, E. E. Ituen, A. N. Ikot, O. Ebomwonyi, J. O. Okoro & K. O. Dopamu, “Eigensolutions, Shannon entropy and Information energy for Tietz-Hua potential”, Indian Journal Physics 92 (2018) 487.

S. E. Massen, “Application of information entropy to nuclei”, Physical Review C 67 (2003) 014314.

D. Dutta & P. Roy, “Information entropy for conditionally exactly solvable potentials”, Journal of Mathematical Physics 52 (2011) 032104.

S. Dong, S. G. Sun, S. H. Dong & J. P. Draayer, “Quantum information entropies for a squared tangent potential well”, Physics Letters A 378 (2014) 124.

S. Lopez-Rosa, J. Montero, P. Sanchez-Moreno, J. Venegas & J. S. Dehesa, “Position and momentum information-theoretic measures of a D-dimensional particle in a box”, Journal of Mathematical Chemistry 49 (2011) 971.

G. Yanez-Navarro, G. H. Sun, T. Dytrych, K. D. Lanney, S. H. Dong & J. P. Draayer, “Quantum information entropies for position-dependent mass Schrödinger problem”, Annals of Physics 348 (2014) 153.

S. Liu, “On the relationship between densities of Shannon entropy and Fisher information for atoms and molecules”, Journal of Chemical Physics 126 (2007) 191109.

C. A. Onate, M. C. Onyeaju, A. N. Ikot & O. Ebomwonyi, “Eigen solutions and entropic system for Hellmann potential in the presence of the Schrödinger equation”, European Physical Journal Plus 132 (2017) 462.

Y. P. Varshni & R. C. Shukla, “Potential energy functions for alkali halide molecules” Journal of Molecular Physics 16 (1965) 63.

C. A. Onate, M. C. Onyeaju, A. N. Ikot, O. Ebomwonyi & J. O. A. Idiodi, “Dirac equation with a new tensor interaction under spin and pseudospin symmetries”, Communications in Theoretical Physics 70 (2018) 294.

O. Bayrak, I. Boztosun & H. Ciftci, “Exact analytical solutions to the Kratzer potential by the asymptotic iteration method”, International Journal of Quantum Chemistry, 107 (2007) 540.

C. Tezcan & R. Sever, “A General Approach for the Exact Solution of the Schrödinger Equation”, International Journal of Theoretical Physics 48 (2009) 337.

O. Ebomwonyi, C. A. Onate, M. C. Onyeaju & A. N. Ikot, “Any l-states solutions of the Schrödinger equation interacting with Hellmann-generalized Morse potential model”, Karbala International Journal of Modern Science 3 (2017) 59.

B. J. Falaye, “The Klein-Gordon equation with ring-shaped potentials: Asymptotic iteration method”, Journal of Mathematical Physics 53 (2012) 082107.

B. J. Falaye, “Exact solutions of the Klein-Gordon equation for spherically asymmetrically singular oscillator” Few Body System 53 (2012) 563.

A. D. Antia, A. N. Ikot, I. O. Akpan & O. A. Awoga, “Approximate solutions of the Klein-Gordon equation with unequal scalar and vector modified Hylleraas potential”, Indian Journal of Physics 87 (2013) 155.

A. D. Antia, A. N. Ikot, H. Hassanabadi & E. Maghsoodi, “Bound state solutions of the Klein-Gordon equation with Mobius square plus Yukawa potentials”, Indian Journal of Physics 87 (2013) 1133.

C. N. Isonguyo, I. B. Okon, A. N. Ikot & H. Hassanabadi, “Solutions of Klein-Gordon equation for some diatomic molecules with new generalized Morse-like potential by SUSYQM”, Bulletin Korean Chemimal Society 35 (2014) 3443.

A. N. Ikot, B. C. Lulfuoglu, M. I. Ngwueke, M. E. Udoh, S. Zare & H. Hassanabadi, “Klein-Gordon equation particles in exponential-type molecule potentials and their thermodynamic properties in D-dimensions”, European Physical Journal Plus 131 (2016) 131.

A. N. Ikot, H. Hassanabadi, H. P. Obong, Y. E. C. Umoren & C. N. Isonguyo, “Approximate solutions of the Klein-Gordon equation with improved Manning-Rosen potential in D-dimensions using SUSYQM”, Chinses Physics B 23 (2014) 120303.

C. A. Onate, M. C. Onyeaju, A. N. Ikot & O. J. Ojonubah, “Analytical solutions of the Klein-Gordon equation with a combined potential”, Chinese Journal of Physics 54 (2018) 820.

A. Alhaidari, H. Bahlouli & A. Al-Hassan, “Dirac and Klein–Gordon equations with equal scalar and vector potentials”, Physics Letters A 349 (2006) 87.

C. A. Onate, “Relativistic and nonrelativistic solutions of inversely quandratic Yukawa potential”, African Review of Physics 8 (2013) 325.

C. A. Onate, A. N. Ikot, M. C. Onyeaju & M. E. Udoh, “Bound state solutions of the D-dimensional Klein-Gordon equation with hyperbolic potential”, Karbala International Journal of Modern Science 3 (2017) 1.

C. -S. Jia, T. Chen & S. He, “Bound state solutions of the Klein–Gordon equation with the improved expression of the Manning–Rosen potential energy model”, Physics Letters A 377 (2013) 682.

T, Chen, S. –R. Lin & C. –S. Jia, “Solutions of the Klein-Gordon equation with the improved Rosen-Morse potential energy model”, European Physical Journal Plus 128 (2013) 69.

X. –J. Xie & C. –S. Jia, “Solutions of the Klein–Gordon equation with the Morse potential energy model in higher spatial dimensions”, Physica Scripta 90 (2015) 035207.

B. Tang & C. –S. Jia, “Relativistic spinless rotation-vibrational energies of carbon monoxide”, European Physical Journal Plus 132 (2017) 375.

J. –Y. Liu, J. –F. Du & C. –S. Jia, “Molecular spinless energies of the improved Tietz potential energy model, “European Physical Journal Plus 128 (2013) 139.

X. –Y. Chen, T. Chen & C. –S. Jia, “Solutions of the Klein-Gordon equation with the improved Manning-Rosen potential energy model in D dimensions”, European Physical Journal Plus 129 (2014) 75.

C. –S. Jia, X. –L. Peng & S. He, “Molecular Spinless Energies of the Modified Rosen-Morse Potential Energy Model”, Bulletin of the Korean Chemical Society 35 (2014) 2699.

C. –S. Jia, J. –W. Dai, L. –H. Zhang, J. –Y. Liu & G. –D. Zhang, “Molecular spinless energies of the modified Rosen–Morse potential energy model in higher spatial dimensions”, Chemical Physics Letters 619 (2015) 54.

Han-Bin Liu1 Liang-Zhong Yi2 Chun-Sheng Jia, “Solutions of the Klein–Gordon equation with the improved Tietz potential energy model”, Journal of Mathematical Chemistry 56 (2018) 2982.

A. Rényi, (1961). “On Measures of Entropy and Information”, Proceeding 4 th Berkeley Symposium in Mathematics and Statistical Probability 1 (1961) 547.

C. Tsallis, “Possible generalization of Boltzmann-Gibbs Statistics”, Journal of Statistical Probability 52 (1988) 479.

Shannon entropy for position space

Published

2021-08-29

How to Cite

Entropic system in the relativistic Klein-Gordon Particle. (2021). Journal of the Nigerian Society of Physical Sciences, 3(3), 165–171. https://doi.org/10.46481/jnsps.2021.209

Issue

Volume 3, Issue 3, August 2021

Section

Original Research
Copyright & Licensing

Copyright (c) 2021 Journal of the Nigerian Society of Physical Sciences

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Entropic system in the relativistic Klein-Gordon Particle. (2021). Journal of the Nigerian Society of Physical Sciences, 3(3), 165–171. https://doi.org/10.46481/jnsps.2021.209