Modified Gradient Flow Method for Solving One-Dimensional Optimal Control Problem Governed by Linear Equality Constraint

Olusegun Olotu; Charles  Aladesaye; Kazeem Adebowale Dawodu

doi:10.46481/jnsps.2022.589

Authors

Olusegun Olotu Department of Mathematical Sciences,The Federal University of Technology Akure, Nigeria
Charles Aladesaye Dept. of Mathematics, School of Science, College of Education, Ikere-Ekiti, Ekiti State, Nigeria
Kazeem Adebowale Dawodu
kadawodu@futa.edu.ng
Department of Mathematical Sciences,The Federal University of Technology Akure, Nigeria

Keywords:

Optimal Control, Gradient Flow, three-level splitting parameters, discretization scheme, linear and quadratic convergence

Abstract

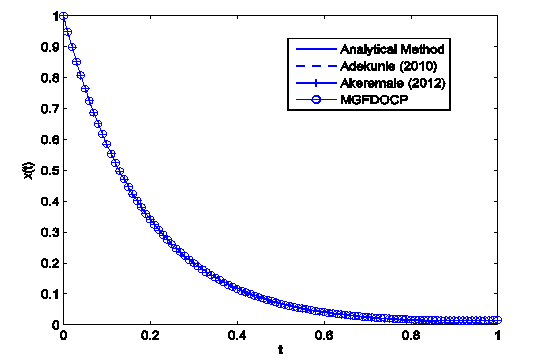
This study presents a computational technique developed for solving linearly constraint optimal control problems using the Gradient Flow Method. This proposed method, called the Modified Gradient Flow Method (MGFM), is based on the continuous gradient flow reformulation of constrained optimization problem with three-level implicit time discretization scheme. The three-level splitting parameters for the discretization of the gradient flow equations are such that the sum of the parameters equal to one (\theta₁ + \theta₂ +\theta₃=1). The Linear and quadratic convergence of the scheme were analyzed and were shown to have first order scheme when each parameter exist in the domain [0, 1] and second order when the third parameter equal to one. Numerical experiments were carried out and the results showed that the approach is very effective for handling this class of constrained optimal control problems. It also compared favorably with the analytical solutions and performed better than the existing schemes in terms of convergence and accuracy

Dimensions

REFERENCES

A. I. Adekunle, “Algorithm for a Class of Discretized Optimal Control Problems", M.Tech. Thesis, Federal University of Technology, Akure, Nigeria (2011) (Unpublished).

O. C. Akeremale, “Optimization of Quadratic Constrained Optimal Control Problems using Augumented Lagrangian Method", M.Tech. Thesis, Federal University of Technology, Akure, Nigeria (2012) (Unpublished)

W. Behrman, “An Effcient Gradient Flow Method for Unconstrained Optimization", PhD Thesis, Stanford University (1998) (Unpublished).

J. T. Betts, “Practical Methods for Optimal Control Problem Using Non linear programming", SIAM, Philadelphia, (2001).

Y. Evtushenko, “Generalized Lagrange Multipliers Technique for Nonlinear Programming", JOTA, 21 (1977) 121. DOI: https://doi.org/10.1007/BF00932516

Y. G. Evtushenko & V. G. Zhadan, “Stable Barrier Projection and Barrier Newton Methods", Nonlinear Programming Optimization Methods and Software, 3 (1994) 237. DOI: https://doi.org/10.1080/10556789408805567

G. T. Gilbert, “Positive Definite Matrices and Sylvester’s Criterion", The American Mathematical Monthly, Taylor & Francis, 98 (1991) 44. DOI: https://doi.org/10.2307/2324036

W. M. Haddad, S. G. Nersesov & V.S. Chellaboina, “Lyapunov Function Proof of Poincare’s Theorem", International Journal of Systems Science, 35 (2004) 287. DOI: https://doi.org/10.1080/00207720410001714824

J. B. Layton, “Efficient direct computatioion of the Pseudo-inverse and its gradient", International Journal for Numerical Methods in Engineering, 40 (1997) 4211. DOI: https://doi.org/10.1002/(SICI)1097-0207(19971130)40:22<4211::AID-NME255>3.0.CO;2-8

W. H. Morris, S. Stephen & L. D. Robert, “Di erential Equations, Dynamical Systems, and an Introduction to Chaos", Elsevier Academic Press, USA (2004) 194.

O. Olotu & K. A. Dawodu, “Quasi-Newton Embedded Augmented Lagrangian Algorithm for Discretized Optimal Proportional Control Problems", Journal of Mathematical Theory and Modeling, 3 (2013a) 67.

O. Olotu & K. A. Dawodu, “On the Discretized Algorithm for Optimal Proportional Control Problems Constrained by Delay Differential Equations", Journal of Mathematical Theory and Modeling, 3 (2013b) 157.

O. Olotu & S. A. Olorunsola, “An Algorithm for a Discretized Constrained, Continuous Quadratic Control Problem", Journal of Applied Sciences, 8 (2006) 6249. DOI: https://doi.org/10.4314/jonamp.v8i1.40017

L. S. Pontryagin, V. G. Boltyanskii, R. V. Gamkrelidze & E. F. Mishchenko, “The Mathematical Theory of Optimal Processes", Interscience Publishers, London (1962).

S. Wang, X. Q. Yang K. L. Teo “A Unified Gradient Flow Approach to Constrained Nonlinear Optimization Problems", Computational Optimization and Applications, 25 (2003) 251. DOI: https://doi.org/10.1023/A:1022973608903