Time-Fractional Differential Equations with an Approximate Solution

Authors

  • Lamees K. Alzaki Department of Mathematics, Faculty of Education for Pure Science, University of Thi-Qar, Nasiriyah, Iraq.
  • Hassan Kamil Jassim Department of Mathematics, Faculty of Education for Pure Science, University of Thi-Qar, Nasiriyah, Iraq.

Keywords:

Fractional differential equations, Homotopy perturbation method, Sumudu transform

Abstract

This paper shows how to use the fractional Sumudu homotopy perturbation technique (SHP) with the Caputo fractional operator (CF) to solve time fractional linear and nonlinear partial differential equations. The Sumudu transform (ST) and the homotopy perturbation technique (HP) are combined in this approach. In the Caputo definition, the fractional derivative is defined. In general, the method is straightforward to execute and yields good results. There are some examples offered to demonstrate the technique's validity and use.

Dimensions

G. Aguilar, Y. Martinez, T. Jimenez, C. Fraga, E. Jimenez, O. Peregrino, Homotopy perturbation transform method for nonlinear differential equations involving to fractional operator with exponential kernel, Advances in Difference Equations 68 (2017) 1.

L. Debnath, A brief historical introduction to fractional calculus, Int. J. Math. Educ. Sci. Technol. 35 (2004) 487.

N. I. Mahmudov, M. Awadalla, K. Abuassba, Nonlinear sequential fractional differential equations with nonlocal boundary conditions, Advances in Difference Equations 319 (2017) 1.

I. Podlubny, Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, 198. Elsevier, Amsterdam (1998).

R. Almeida, N. R. Bastos, Modeling some real phenomena by fractional differential equations, Math.Methods Appl. Sci. 39 (2016) 4846.

R. Almeida, A. B. Malinowska, M. T. Monteiro Fractional differential equations with a Caputo derivative with respect to a kernel function and their applications, Math. Methods Appl. Sci. 41 (2018) 336.

J.-H. He, Homotopy perturbation technique, Computer Methods in Applied Mechanics and Engineering 178 (1999) 257.

S. A. El-Wakil, A. Elhanbaly, M. A. Abdou, Adomian decomposition method for solving fractional nonlinear partial differential equations, Applied Mathematics and Computation 182 (2006) 313.

M. M. El-Borai, W. G. El-Sayed, A. M. Jawad,Adomian decomposition method for solving fractional differential equations, International Research Journal of Engineering and Technology 2 (2015) 296.

Z. P. Fan, H. K. Jassim, R. K. Rainna, and X. J. Yang, Adomian Decomposition Method for Three-Dimensional Diffusion Model in Fractal Heat Transfer Involving Local Fractional Derivatives, Thermal Science 19 (2015) S137.

A. Yildir?m, A. K. Akbay, Homotopy perturbation method for numerical solutions of coupled Burger’s equations with time-space fractional derivatives. International Journal of Numerical Methods for Heat and Fluid Flow 20 (2010) 897.

J. Singh, D. Kumar, R. Swroop, Numerical solution of time- and spacefractional coupled Burger’s equations via homotopy algorithm, Alexandria Engineering Journal 55 (2016) 1753.

S. Momani, A. Yildirim A, Analytical approximate solutions of the fractional convection diffusion equation with nonlinear source term by homotopy perturbation method, Int. J. Comput. Math. 87 (2010) 1057.

S. Q. Wang, Y. J. Yang, and H. K. Jassim, Local Fractional Function Decomposition Method for Solving Inhomogeneous Wave Equations with Local Fractional Derivative, Abstract and Applied Analysis, 2014 (2014) 1.

S. P. Yan, H. Jafari, and H. K. Jassim, Local Fractional Adomian Decomposition and Function Decomposition Methods for Solving Laplace Equation within Local Fractional Operators,Advances in Mathematical Physics 2014 (2014) 1.

S. Xu, X. Ling, Y. Zhao, H. K. Jassim, A Novel Schedule for Solving the Two-Dimensional Diffusion in Fractal Heat Transfer, Thermal Science 19 (2015) S99.

H. K. Jassim, W.A. Shahab, Fractional variational iteration method to solve one dimensional second order hyperbolic telegraph equations, Journal of Physics: Conference Series 1032 (2018) 1.

H. Jafari, H. K. Jassim, J. Vahidi,Reduced Differential Transform and Variational Iteration Methods for 3D Diffusion Model in Fractal Heat Transfer within Local Fractional Operators, Thermal Science 22 (2018) S301.

H. Jafari, H. K. Jassim, S. P. Moshokoa, V. M. Ariyan and F. Tchier, Reduced differential transform method for partial differential equations within local fractional derivative operators, Advances in Mechanical Engineering 8 (2016) 1.

M. S. Rawashdeh, A reliable method for the space-time fractional Burgers and time-fractional Cahn-Allen equations via the FRDTM, Advances in Difference Equations 99 (2017) 1.

H. K. Jassim, J. Vahidi, A New Technique of Reduce Differential Transform Method to Solve Local Fractional PDEs in Mathematical Physics, International Journal of Nonlinear Analysis and Applications 12 (2021) 37.

H. Jafari, H. K. Jassim, F. Tchier, D. Baleanu, On the Approximate Solutions of Local Fractional Differential Equations with Local Fractional Operator, Entropy 18 (2016) 1.

D. Baleanu, H. K. Jassim, Approximate Analytical Solutions of Goursat Problem within Local Fractional Operators, Journal of Nonlinear Science and Applications 9 (2016) 4829.

H. K. Jassim, J. Vahidi, V. M. Ariyan, Solving Laplace Equation within Local Fractional Operators by Using Local Fractional Differential Transform and Laplace Variational Iteration Methods, Nonlinear Dynamics, and Systems Theory 20 (2020) 388.

H. K. Jassim, New Approaches for Solving Fokker Planck Equation on Cantor Sets within Local Fractional Operators, Journal of Mathematics 2015 (2015) 1.

H. K. Jassim, C. U¨ nlu¨, S. P. Moshokoa, C. M. Khalique, Local Fractional Laplace Variational Iteration Method for Solving Diffusion and Wave Equations on Cantor Sets within Local Fractional Operators, Mathematical Problems in Engineering, 2015 (2015) 1.

H. K. Jassim, The Approximate Solutions of Three-Dimensional Diffusion and Wave Equations within Local Fractional Derivative Operator, Abstract and Applied Analysis 2016 (2016) 2913539.

H. Jafari, H. K. Jassim, On the Existence and Uniqueness of Solutions for Local differential equations, Entropy 18 (2016) 1.

D. Baleanu, H. K. Jassim, H. Khan, A Modification Fractional Variational Iteration Method for solving Nonlinear Gas Dynamic and Coupled KdV Equations Involving Local Fractional Operators, Thermal Science 22 (2018) S165.

H. K. Jassim, D. Baleanu, A novel approach for Korteweg-de Vries equation of fractional order, Journal of Applied Computational Mechanics 5 (2019) 192.

D. Baleanu, H. K. Jassim, M. Al Qurashi,Solving Helmholtz Equation with Local Fractional Derivative Operators, Fractal and Fractional 3 (2019) 1.

D. Baleanu, H. K. Jassim, Approximate Solutions of the Damped Wave Equation and Dissipative Wave Equation in Fractal Strings, Fractal and Fractional 3 (2019) 1.

D. Baleanu, H. K. Jassim, A Modification Fractional Homotopy Perturbation Method for Solving Helmholtz and Coupled Helmholtz Equations on Cantor Sets, Fractal and Fractional 3 (2019) 1.

H. K. Jassim, Analytical Approximate Solutions for Local Fractional Wave Equations, Mathematical Methods in the Applied Sciences 43 (2020) 939.

J. Singh, H. K. Jassim, D. Kumar, An efficient computational technique for local fractional Fokker-Planck equation, Physica A: Statistical Mechanics and its Applications, 555 (124525) (2020) 1.

H. K. Jassim, M. G. Mohammed, H. A. Eaued, , A Modification Fractional Homotopy Analysis Method for Solving Partial Differential Equations Arising in Mathematical Physics, IOP Conf. Series: Materials Science and Engineering 928 (2020) 042021.

H. A. Eaued, H. K. Jassim, M. G. Mohammed, A Novel Method for the Analytical Solution of Partial Differential Equations Arising in Mathematical Physics, IOP Conf. Series: Materials Science and Engineering 928 (2020) 042037.

H. K. Jassim, S. A. Khafif, SVIM for solving Burger’s and coupled Burger’s equations of fractional order, Progress in Fractional Differentiation and Applications 7 (2021) 1.

H. K. Jassim, H. A. Kadhim, Fractional Sumudu decomposition method for solving PDEs of fractional order, Journal of Applied and Computational Mechanics 7 (2021) 302-311.

D. Baleanu, H. K. Jassim, Exact Solution of Two-dimensional Fractional Partial Differential Equations, Fractal Fractional 4 (2020) 1.

H. K. Jassim, M. A. Shareef, On approximate solutions for fractional system of differential equations with Caputo-Fabrizio fractional operator, Journal of Mathematics and Computer science 23 (2021) 58.

H. Jafari, H. K. Jassim, D. Baleanu, Y. M. Chu, SOn the approximate solutions for a system of coupled Korteweg-de Vries equations with local fractional derivative, Fractals 29 (2021) 1.

H. K. Jassim, M. G. Mohammed, Natural homotopy perturbation method for solving nonlinear fractional gas dynamics equations, International Journal of Nonlinear Analysis and Applications 12 (2021) 37.

H. K. Jassim, A new approach to find approximate solutions of Burger’s and coupled Burger’s equations of fractional order, TWMS Journal of Applied and Engineering Mathematics, 11(2) (2021) 415-423.

L. K. Alzaki, H. K. Jassim, The approximate analytical solutions of nonlinear fractional ordinary differential equations, International Journal of Nonlinear Analysis and Applications 12 (2021) 527.

I. Mehdipour, D.D.Ganji, M. Mozaffari, Application of the energy balance method to nonlinear vibrating equations, Current Applied Physics 10 (2010) 104.

H. M. Hasson, Power series method for solving nonlinear Volterra integro-differential equations of the second kind, Engineering and Technology Journal 28 (2010) 4816.

S. E. Fadugba, Solution of Fractional Order Equations in the Domain of the Mellin, Transform. Journal of the Nigerian Society of Physical Sciences 1 (2019), 138–142.

V. J. Shaalini, S. E. Fadugba, A New Multi-Step Method for Solving Delay Differential Equations using Lagrange Interpolation, Journal of the Nigerian Society of Physical Sciences 3 (2010), 159–164.

J. Kuboye, O. R. Elusakin, O. F. Quadri, Numerical Algorithms for Direct Solution of Fourth Order Ordinary Differential Equations, Journal of the Nigerian Society of Physical Sciences 2 (2020) 218.

J. O. Kuboye, O. F. Quadri, O. R. Elusakin, Solving third order ordinary differential equations directly using hybrid numerical models, Journal of the Nigerian Society of Physical Sciences 2 (2020), 69.

Y.Ibrahim, Strong Convergence Theorems for Split Common Fixed Point Problem of Bregman Generalized Asymptotically Nonexpansive Mappings in Banach Spaces, Journal of the Nigerian Society of Physical Sciences 1 (2019) 35.

K.Wang, S. Liu, A new Sumudu transform iterative method for time fractional Cauchy reaction diffusion equation, Advances in Difference Equations 5 (865) (2016) 1.

A.K. Alomari, Homotopy-Sumudu transforms for solving system of fractional partial differential equations,Advances in Difference Equations 1 (2020) 222.

H. Eltayeb, A. Kilicmai, A note on the Sumudu transform and DEs, Applied Math. Sci. 4 (2010) 1089

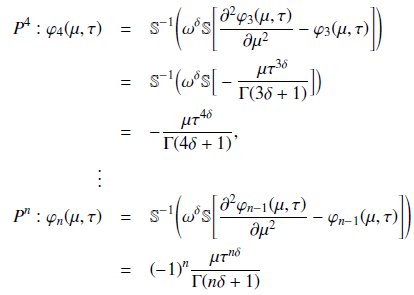
Published

2022-08-18

How to Cite

Time-Fractional Differential Equations with an Approximate Solution. (2022). Journal of the Nigerian Society of Physical Sciences, 4(3), 818. https://doi.org/10.46481/jnsps.2022.818

Issue

Volume 4, Issue 3, August 2022

Section

Original Research
Copyright & Licensing

Copyright (c) 2022 Lamees K. Alzaki, Hassan Kamil Jassim

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Time-Fractional Differential Equations with an Approximate Solution. (2022). Journal of the Nigerian Society of Physical Sciences, 4(3), 818. https://doi.org/10.46481/jnsps.2022.818