The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method
Keywords:
Dengue Fever, Mathematical Model, Differential Transformation Method, Ordinary Differential EquationsAbstract
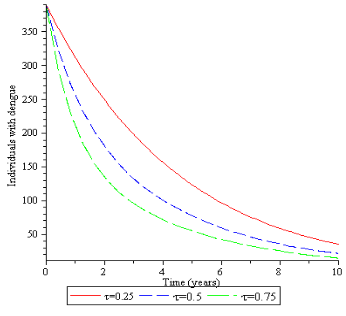
Differential Transformation Method (DTM) is a very effective tool for solving linear and non-linear ordinary differential equations. This paper uses DTM to solve the mathematical model for the dynamics of Dengue fever in a population. The graphical profiles for human population are obtained using Maple software. The solution profiles give the long term behavior of Dengue fever model which shows that treatment plays a vital role in reducing the disease burden in a population.
Dimensions
Published
2019-09-03
How to Cite
The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method. (2019). Journal of the Nigerian Society of Physical Sciences, 1(3), 82-87. https://doi.org/10.46481/jnsps.2019.18
Issue
Section
Original Research
Copyright & Licensing
Copyright (c) 2019 Journal of the Nigerian Society of Physical Sciences
This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method. (2019). Journal of the Nigerian Society of Physical Sciences, 1(3), 82-87. https://doi.org/10.46481/jnsps.2019.18
Similar Articles
- Gurpreet Tuteja, Tapshi Singh, Comments on “The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method: J. Nig. Soc. Phys. Sci. 1 (2019) 82-87” , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 2, May 2021
- Ogechi Regina Amanso, Jeconia Okelo Abonyo, Phineas Roy Kiogora, Obiora Cornelius Collins, A novel mathematical model for transmission dynamics of HPV and cervical cancer progression with cancer-reliant awareness , Journal of the Nigerian Society of Physical Sciences: Volume 8, Issue 2, May 2026
- Dalal Khalid Almutairi, Mohamed A. Abdoon, Salih Yousuf Mohamed Salih, Shahinaz A.Elsamani, Fathelrhman EL Guma, Mohammed Berir, Modeling and Analysis of a Fractional Visceral Leishmaniosis with Caputo and Caputo–Fabrizio derivatives , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 3, August 2023
- S. Alao , R. A. Oderinu, B. A. Sanusi, T. A. Oyeyinka, F. J. Ayanbukola, Computational investigation of magnetohydrodynamics Casson Micropolar fluid flowing past a permeable linearly stretchy wall with heat source , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 3, August 2025
- J. Andrawus, J. Y. Musa, S. Babuba, A. Yusuf, S. Qureshi, U. T. Mustapha, A. Oghenefejiro, I. S. Mamba, Modeling the dynamics of pertussis to assess the influence of timely awareness with optimal control analysis , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 4, November 2025
- Friday Obarhua, Oluwasemire John Adegboro, An Order Four Continuous Numerical Method for Solving General Second Order Ordinary Differential Equations , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 1, February 2021
- Solomon A. Ayuba, I. Akeyede, A. S. Olagunju, Stability and Sensitivity Analysis of Dengue-Malaria Co-Infection Model in Endemic Stage , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 2, May 2021
- Maduabuchi Gabriel Orakwelu, Olumuyiwa Otegbeye, Hermane Mambili-Mamboundou, A class of single-step hybrid block methods with equally spaced points for general third-order ordinary differential equations , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 4, November 2023
- Peter Urane Achimugwu, Mathew Ngugi Kinyanjui, David Mumo Malonza, Analysis of a fractional order climate model due to excessive emission and accumulation of carbon dioxide in the atmosphere , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 4, November 2023
- Mark I. Modebei, Olumide O. Olaiya, Ignatius P. Ngwongwo, Computational study of a 3-step hybrid integrators for third order ordinary differential equations with shift of three off-step points , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 4, November 2021
1-10 of 314
Next
You may also start an advanced similarity search for this article.
Most read articles by the same author(s)
- James Andrawus, Kayode Isaac Omotoso, Agada Apeh Andrew, Felix Yakubu Eguda, Sunday Babuba, Kabiru Garba Ibrahim, Mathematical model analysis on the significance of surveillance and awareness on the transmission dynamics of diphtheria , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 4, November 2025
