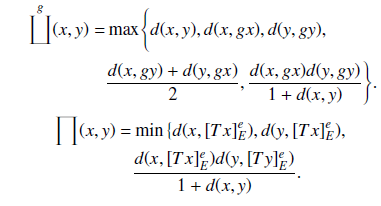On Fuzzy Soft Set-Valued Maps with Application

Authors

Keywords:

Soft set, Fuzzy soft set, Fuzzy soft set-valued map, Fuzzy soft fixed point, Weak contraction

Abstract

Soft set and fuzzy soft set theories are proposed as mathematical tools for dealing with uncertainties. There has been tremendous progress concerning the extensions of these theories from different point of views of researchers so as to accommodate more robust and expressive applications in everyday life. In line with this development, in this paper, we combine the two aforementioned notions to initiate a novel concept of set-valued maps whose range set is a family of fuzzy soft sets. The later idea is employed to define Suzuki-type fuzzy soft $(e,K)$-weak contractions, thereby establishing some related fuzzy soft fixed point theorems. As a consequence, several well-known Suzuki-type fixed point theorems are derived as corollaries. Examples are also provided to validate the new concepts and to support the authenticity of the obtained results. Moreover, an application in homotopy is considered to show the usability of the obtained results.

Dimensions

S. Banach,“ Sur les op´erations dans les ensembles abstraits et leur application aux ´equations int´egrales”, Fund. math. 3 (1922) 133.

A. Azam, M. Arshad & I. Beg, “Banach contraction principle on cone

rectangular metric spaces”, Applicable Analysis and Discrete Mathematics 3 (2009) 236.

A. Azam, B. Fisher & M. Khan, “Common fixed point theorems in complex valued metric spaces” Numerical Functional Analysis and Optimization 32 (2011) 243.

J. Caristi, “Fixed point theorems for mappings satisfying inwardness conditions”, Transactions of the American Mathematical Society 215 (1976) 251.

L. B. Ciric, “A generalization of Banach’s contraction principle”, Proceedings of the American Mathematical society 45 (1974) 267.

A. Meir & E. Keeler, “A theorem on contraction mappings”, Journal of Mathematical Analysis and Applications 28 (1969) 326.

S. B. Nadler, “Multi-valued contraction mappings”, Pacific Journal of Mathematics 30(1969) 475.

A. Azam & M. Arshad, “Kannan fixed point theorem on generalized metric spaces”, The Journal of Nonlinear Sciences and Its Applications 1 (2008) 45.

S.K. Chatterjea, “Fixed point theorems”, Acad. Bulgare Sci. 25 (1972) 727.

Y. Ibrahim, “ Common Fixed Point Theorems for Multivalued Generalized F-Suzuki-Contraction Mappings in Complete Strong b-Metric Spaces”, Journal of the Nigerian Society of Physical Sciences 1 (2019) 88.

I. A. Rus, “Generalized contractions and applications”, Cluj University Press 4 (2001)8.

T, Zamfirescu, “Fixed point theorems in metric spaces”, Archiv der Mathematik 23 (1972) 292.

V. Berinde, “Approximating fixed points of weak contractions using the Picard iteration”, In Nonlinear Analysis 9(2004) 43.

M. Berinde & V. Berinde, “On a general class of multi-valued weakly Picard mappings”, Journal of Mathematical Analysis and Applications 326 (2007) 772.

N. C¸ a˘gman & S. Engino˘glu, “Soft set theory and uni–int decision making”, European Journal of Operational Research 207 (2010) 848.

D. Doric & R. Lazovic, “Some Suzuki-type fixed point theorems for generalized multivalued mappings and applications”, Fixed Point Theory and Applications 1 (2011) 40.

Q. Feng & Y. Zhou, “Soft discernibility matrix and its applications in decision making”, Applied Soft Computing 24(2014) 749.

R. Kannan, “Some results on fixed points—II’, The American Mathematical Monthly, 76(1969) 405.

M. Kikkawa, & T. Suzuki, “Some similarity between contractions and Kannan mappings”, Fixed Point Theory and Applications 2008 (2008) 649749.

Z. Kong, L. Gao, & L. Wang, “Comment on: A fuzzy soft set theoretic approach to decision making problems”, Journal of computational and applied mathematics 223 (2009) 540.

P. K. Maji, P. Biswas & A. R. Roy. “Fuzzy soft sets”, Journal of fuzzy mathematics 6(2001) 9.

X. Yang, D. Yu, J. Yang & C.Wu, “Generalization of soft set theory: from crisp to fuzzy case”, In Fuzzy Information and Engineering 3(2007) 345.

P. K. Maji, A. R. Roy, & R. Biswas, “An application of soft sets in a decision making problem”, Computers and Mathematics with Applications 44 (2002) 1077.

Roy, A. R. & Maji, P. K., “A fuzzy soft set theoretic approach to decision making problems”, Journal of Computational and Applied Mathematics 203 (2007) 412.

S. S. Mohammed & A. Azam, “An algorithm for fuzzy soft set based decision making approach”, Yugoslav Journal of Operations Research 30 (2020) 59.

D. Molodtsov, “Soft set theory—first results”, Computers and Mathematics with Applications 37 (1999) 19.

Z. Pawlak, “Rough sets”, International journal of computer and information sciences 11 (1982) 341.

P. V. Subrahmanyam, “Remarks on some fixed point theorems related to Banach’s contraction principle”, J. Math. Phys. Sci. 8 (1974) 445.

T. Suzuki, “A generalized Banach contraction principle that characterizes metric completeness”, Proceedings of the American Mathematical Society 136 (2008) 1861.

L. A. Zadeh, “Fuzzy sets”, Information and control 8 (1965) 338.

Published

2020-02-28

How to Cite

On Fuzzy Soft Set-Valued Maps with Application. (2020). Journal of the Nigerian Society of Physical Sciences, 2(1), 26-35. https://doi.org/10.46481/jnsps.2020.48

Issue

Volume 2, Issue 1, February 2020

Section

Original Research
Copyright & Licensing

How to Cite

On Fuzzy Soft Set-Valued Maps with Application. (2020). Journal of the Nigerian Society of Physical Sciences, 2(1), 26-35. https://doi.org/10.46481/jnsps.2020.48